问题十一
整数划分问题
问题描述:
输出正整数的划分情况
问题举例:
待划分数:4
划分情况:
3+1
2+2
2+1+1
1+1+1+1
思路分析:
整数划分问题是一个经典的递归问题,递归问题最重要的部分就是寻找递归函数和递归终止条件。在本问题中,通过分析,我们能将划分问题分解成这四种情况。我们设函数为divide(n,m),其中n是待划分的数,m是最大加数的值,比如m设置为1,则就只能分解成n个1相加这一种情况。所以divide(n,1)就是第一种情况,当n或者m为1时触发此种情况。当m>n时,由于m不能大于待划分的数,所以其等价于divide(n,n);当m=n时,此时最大加数由n-1构成,比如divide(4,4)则自然最大加数应该是3,而不是4,故n-1。最后一种情况是m<n,也就是最正常的情况,此时divide(n,m)=divide(n,m-1)+divide(n-m,m),这个式子由两部分组成,第一个divide(n,m-1)是指划分中不包含最大加数m的情况,所以此时所有的划分都比最大加数小,也就是从n中取最大为m-1的数值;第二个divide(n-m,m)是指划分中包含最大加数m的情况,由于在n-m中可能会再次出现m,所以这里的划分个数是divide(n-m,m)。
总结: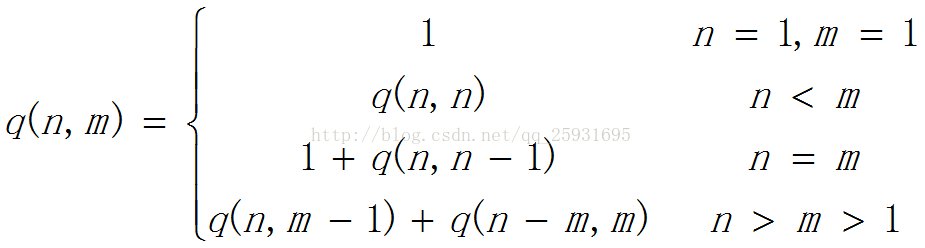
代码实现:
1 | public class NumberDivide { |
分析:
上述方法就是按照标准递归写法完成的实现,其中当n或m为1的时候就退出,其余时候就递归。
但是上述方法输出的只是划分的结果是多少种,而不能按照我们心中所期望的那样,把每种划分情况进行输出,不利于对划分是否正确进行观察,所以这里给出第二份实现代码。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29public class NumberDivide2 {
private static int[] mark=new int[100];
private static int n=4;
private void divide(int now,int k,int pre){
int i;
if (now>n)
return;
if (now==n){
System.out.printf("%d=",n);
for (i=0;i<k-1;i++){
System.out.printf("%d+",mark[i]);
}
System.out.printf("%d\n",mark[i]);
}else {
for (i=pre;i>0;i--){
mark[k]=i;
now+=i;
divide(now,k+1,i);
now-=i;
}
}
}
public static void main(String[] args) {
NumberDivide2 nd2 = new NumberDivide2();
nd2.divide(0,0,n-1);
}
}

分析:
上面的运行结果清晰的表明了划分的结果,我们来分析一下上面的代码,其中mark数组用于存放划分出来的数,这里只是设置成了100的大小。也就是说这个程序目前可以计算100以及以内的划分,101会因为101个1相加而使mark数组越界。n代表了待划分的数据,之后就进入了递归函数之中,我们通过一张图来解释发生了什么,以n=4,也就是4的划分作为例子。(查看大图)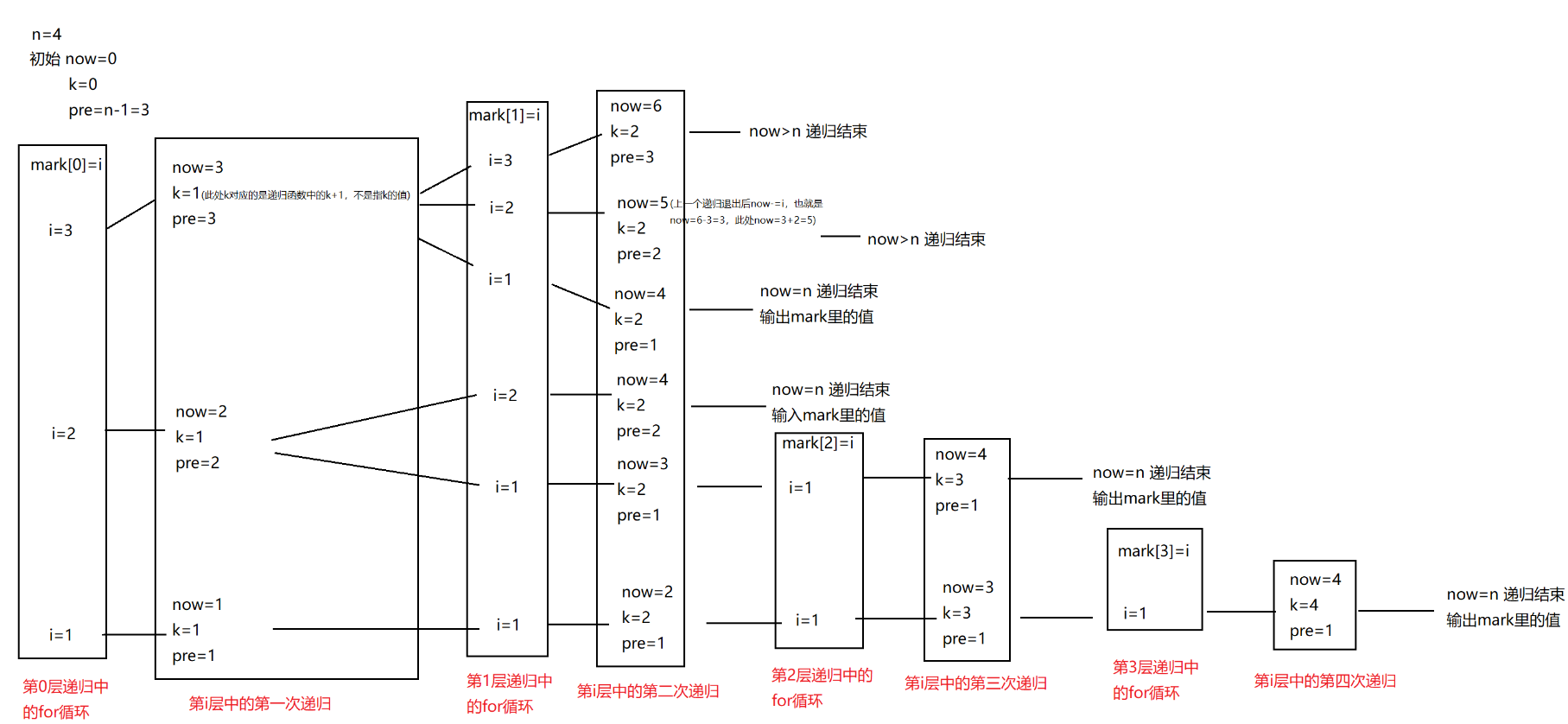
在这个运行过程中,我们可以看到多层递归,所以一定要清楚地认识到我们目前处于哪层递归,以及退出递归后各个变量的数据是多少,否则对递归的理解会出现偏差。
最先进入的参数是divide(0,0,3),由于now<n,所以进入for循环,i=3时,第一次递归时divide(3,1,3),此时循环内的i受pre支配,进入循环后先给mark赋值,用于记录当前的划分值。赋值之后就是修改now的值,now这个值的用途是记录当前mark数组值的和是否与待划分的n相同,如果相同则能保证在下一个递归中输出。之后就是进入下一层递归,注意退出递归后的now-=i的操作,这也就是说要消除之前将当前mark[i]的值加入后带来的影响,从而回归到未加入当前mark值的状态,比如当mark[1]=1时,now=4,此时输出4=3+1,然后递归结束,此时now的值就是4-1=3,这个时候退出的是第二层递归,其实它此时仍然在i=3所在的第一层递归中,此时仍然要执行now-=i的操作,此时now=3,i=第一次递归中的i也即是pre=3,所以now退回到最顶层之后就是0,然后此时开始执行顶层for循环,也就是第0层的i变成2,继续重复上面的操作。k在这个里面的作用就是记录递归层数,每递归一层就为mark[k]赋值。
问题十二:
打靶问题
问题描述:
给定环数和打靶次数,输出有多少种组合能够满足要求。
问题描述:
一共打6次,总环数为45环(每次打靶得分从0到10),共有14748种情况。
思路分析:
这个问题其实很好理解,就是一个次数减少,分数不断增加的计算过程,其中递归退出的条件就是题目要求的打靶次数用尽或者分数达到规定的要求,而我们只要从0环开始进行计算,暴力求解即可完成,只要最后一次打靶前,其总和加上10能达到分数的要求,则代表此次运算成立,组合情况加1。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public class Shoot {
private static int sum=0;
private static int score = 45;
private static void shoot(int num,int scores){
if (num<=0||scores>score)
return;
if (num==1){
if (scores+10>=score)
sum++;
}
for (int i=0;i<=10;++i){
shoot(num-1,scores+i);
}
}
public static void main(String[] args) {
shoot(6,0);
System.out.println(sum);
}
}
分析:
按照思路中所描述的情况进行实现,代码整体比较清晰简单。
问题十三:
八皇后问题
问题描述:
n皇后问题是一个经典的问题,此处讨论八皇后问题,这个问题就是说在棋盘上放置八个皇后,而根据国际象棋的规则,如果某个位置放置了皇后,则其同行、同列、同主对角线、同副对角线则不能再出现皇后,否则就违反规则。
问题举例:
八皇后问题的总共摆法有92种。
思路分析:
八皇后问题是一个经典的递归问题,其主要分为两个部分,那就是摆放和判断部分,我们假设有一个8*8的棋盘,最开始放置的是第0行,那么正常来说,我们就会把第0行的第0到7号位都放置一次,然后以每个位置为基准进行递归,探索第1行、第2行…一直到第7行摆放完毕,如果有冲突则回退上一层,重新为上一层找新的位置。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49public class EightQueen {
private static int dims = 8;
private static int count = 0;
private static int[][] queen = new int[dims][dims];
private boolean isValid(int row,int col){
//判断列冲突
for (int i = 0; i<row; i++)
if (queen[i][col] == 1)
return false;
//判断主对角线冲突
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--)
if (queen[i][j] == 1)
return false;
//判断副对角线冲突
for (int i = row - 1, j = col + 1; i >= 0 && j<dims; i--, j++)
if (queen[i][j] == 1)
return false;
return true;
}
private void Queen(int i)
{
//到达指定维数,进行输出
if (i == dims){
for (int m = 0; m<dims; m++) {
for (int n = 0; n<dims; n++)
System.out.print(queen[m][n]+" ");
System.out.println();
}
System.out.println();
count++;
}
else
for (int j = 0; j<dims; j++)
{
queen[i][j] = 1;
if (isValid(i, j))
Queen(i + 1);
queen[i][j] = 0;
}
}
public static void main(String[] args) {
EightQueen eq = new EightQueen();
eq.Queen(0);
System.out.println("八皇后问题共有"+count+"种解法\n");
}
}
分析:
这段代码主要是分成了两部分,一个是isValid用于判断该位置是否会导致和原有皇后存在冲突,而Queen函数就是递归函数,进行一层一层的查找,最主要的部分就是Queen函数中的for循环,这个循环中首先使用queen[i][j]=1,为当前位置进行赋值,然后把当前位置放入判断函数进行判断是否能够存放,如果可以则进入下一行进行查找,如果不能存放,则将该位置为0,恢复到未放置状态,然后退出当层递归。