算法问题解决(四)

问题五
字符串编辑距离(Levenshtein Distance)

问题描述：
找到字符串的编辑距离，所谓编辑距离就是指由一个字符串通过几次操作(“修改”、“删除”、“添加”)能够变成另外一个字符串，这个方法可以用来处理搜索时的模糊查询，通过判断两个字符串的相近程度给出推荐。

问题举例：
字符串：abc和def的编辑距离是3，因为每个字符对应修改就行；cafe和coffee的编辑距离也是3，只要a替换o，并且增加一个f和一个e即可完成从cafe到coffee的变化。

思路分析：
我们可以以dp[i,j]代表从字符串a的第i个前缀到字符串b的第j个前缀的编辑距离，比如“abc”到“def”的距离为d[3,3]，则代表d[3,3]的值就是最终的编辑距离。
情况一：a的第i位与b的第j位相同，比如“abc”和“dec”，此时d[3,3]=2，而其最后一个字符相同，也就是说不需要转换，则d[i,j]=d[i-1,j-1]。
情况二：a的第i位与b的第j位不同，比如由“abc”转化为“def”可以转化成多种方式，比如abc各位进行替换成def，也可以先添加末尾的f使得abc变成abcf，然后再对前面的元素进行删除等操作，所以在abc后面加上f，则相当于a增加了1，即d[i,j]=d[i,j-1]+1。同理，若在b后面增加1，即d[i,j]=d[i-1,j]+1，如果是修改末尾字符，则相当于d[i,j]=d[i-1,j-1]+1，正因为有如此多的修改方式，所以在选取时需要考虑最小的情况，也就是修改所需步骤最短的一条路。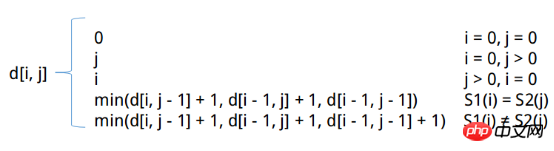

由上图可以得到推到公式，所以就由此公式进行方法的实现。

代码实现：

public class LevenshteinDistance {
    private void levenshtein(String a,String b){
        int[][] dp = new int[a.length()+1][b.length()+1];
        for (int i=1;i<=a.length();i++)
            dp[i][0] = i;
        for (int j=1;j<=b.length();j++)
            dp[0][j] = j;
        for (int i=1;i<=a.length();i++)
            for (int j=1;j<=b.length();j++){
                if(a.charAt(i-1)==b.charAt(j-1))
                    dp[i][j] = min(dp[i-1][j-1],min(dp[i][j-1]+1,dp[i-1][j]+1));
                else
                    dp[i][j] = min(dp[i-1][j-1]+1,min(dp[i][j-1]+1,dp[i-1][j]+1));
            }
        for (int[] d:dp){
            for (int s:d){
                System.out.print(s+" ");
            }
            System.out.println();
        }
    }

    private int min(int a,int b){
        return a>b?b:a;
    }

    public static void main(String[] args) {
        LevenshteinDistance ld = new LevenshteinDistance();
        ld.levenshtein("cafe","coffee");
    }
}

上述代码实现了之前提到的公式，并且对编辑距离求解的过程表进行了输出便于比较和理解。

从上图能够清楚看到每一步的变化以及最后的选择，其中该表右下加的数值即为所求。