问题四
最长递增子序列(Longest Increasing Subsequences)
问题描述:
找到最长递增子序列(之一)
问题举例:
数组:35,36,39,3,15,27,6,42
最长递增子序列(之一):35 36 39 42
思路分析一:
这个问题可以使用两种思路进行解决,第一种就是将问题转化为LCS(最长公共子序列),具体方法就是将待使用的序列进行排序,这样就能将原序列和排序后的序列得到最长公共子序列,这样就能保证子序列是递增的。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25public class LongestIncreasingSubsequence {
private void LIS(String s){
LongestCommonSubsequence lcs = new LongestCommonSubsequence();
lcs.LCS(s,sortString(s));
}
private String sortString(String s){
char[] c = s.toCharArray();
for(int i=0;i<c.length-1;i++){
for(int j=0;j<c.length-i-1;j++){
if(c[j]>c[j+1]){
char temp = c[j];
c[j] = c[j+1];
c[j+1] = temp;
}
}
}
return String.valueOf(c);
}
public static void main(String[] args) {
LongestIncreasingSubsequence lis = new LongestIncreasingSubsequence();
lis.LIS("425781");
}
}
上述代码使用了之前的LCS方法,只是对序列进行了排序,排序方法是采用了简单的冒泡排序,可以采用其他排序方法进行排序。
思路分析二:
另外一个思路就是直接对序列进行查找,其中使用了动态规划的思想。因为L(j)={max(L(i))+1,i小于j且a[i]小于a[j]},所以我们先利用这个思路进行实现。
代码实现二:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62public class LongestIncreasingSubsequence_DPVer {
private static int lis(int [] array)
{
int[] lis = new int[array.length];
int[] pre=new int[array.length];
for(int i =0;i<array.length;i++) {
lis[i]=1;
pre[i]=i;
}
System.out.print("array:");
for(int arr:array){
System.out.print(arr+" ");
}
System.out.println();
for (int j=1; j<array.length; j++) {
for (int i=0; i<j; i++) {
if (array[j]>array[i] && lis[j]<lis[i]+1){
lis[j] = lis[i] + 1;
pre[j]=i;
}
}
}
System.out.print("lis:");
for(int n:lis){
System.out.print(n+" ");
}
System.out.println();
System.out.print("pre:");
for (int m:pre){
System.out.print(m+" ");
}
System.out.println();
int max=0,index = 0;
System.out.print("index:");
for(int k=0;k<lis.length;k++)
{
if(lis[k]>max){
max=lis[k];
index=k;
System.out.print(index+" ");
}
}
System.out.println();
System.out.println("最长递增子序列长度:"+max);
Stack<Integer> stack=new Stack<>();
while(index!=pre[index]){
stack.push(array[index]);
index=pre[index];
}
if(index==pre[index])
stack.push(array[index]);
while(!stack.isEmpty())
System.out.print(stack.pop()+" ");
return max;
}
public static void main(String[] args){
int[] array={43,36,39,47,3,15,27,6,28,49};
lis(array);
}
}
代码分析:
从代码中我们能够看到使用了一个lis数组和一个pre数组,其中这个lis数组是用于统计以array[j]结尾的序列的最长递增子序列长度,而pre数组用于保存子序列中前一个元素所在的位置。如果这么解释比较抽象,那么就通过具体的例子来解释。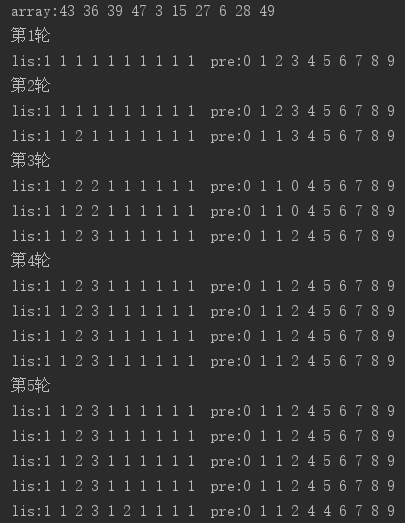
这是通过统计lis和pre数组的变化来进行分析。第一轮是36和43相比,36较小所以lis和pre未更新。第二轮是先用39和43比较,还是小,所以第一次没有变化,再用39和36比较,此时39较大,所以39所在的下标为2的lis值变成了lis[1]+1,变成了2,同时pre数组中39所在的下标为2 的值变成了1。以上的2代表了目前最长子序列的长度是2,而该子序列最后一个元素的前一个元素所在下标为1。第三轮是相同的分析方法,首先是47和43比,47较大并且lis[3]小于lis[0]+1,所以lis[3]=lis[0]+1,pre[3]=pre[0],然后是47和36比,47较大,但是此时你会发现lis和pre都没有更新,这是因为lis[3]小于lis[1]+1不成立,也就是说如果以47作为子序列的结尾所构成的最长子序列并不比原来+1短,所以不需要更新,简单来说就是43和47已经能够组成一个长度为2的子序列了,此时比较完了36,发现其也只能组成长度为2的子序列,这对于要找到最长子序列没有直接帮助,所以跳过。最后就是47和39比较,47比39大,且发现加入39之后,lis的值能够增大,所以就将39加入子序列,得到36、39、47这个更大的子序列,你也许会说明明43所在的lis值也是1,为什么不是43、39、47这个非递增的子序列,这个问题就是通过pre数组解决的,之前说过pre数组的作用,这时你就知道当以47作为结尾时,其前一个元素的下标是2,也就是39所在位置,而39的前一个元素下标是1,也就是36,当36企图继续向前查找时发现其前一个元素下标也是1,也就是本身,所以终止查找。
以上的说明已经包含了多种情况,比如数值比较结果、lis数值比较结果等内容,后续的lis以及pre值的推导可以参照上述规则自行完成,并且每一轮结束就确定了一个lis和pre位的值。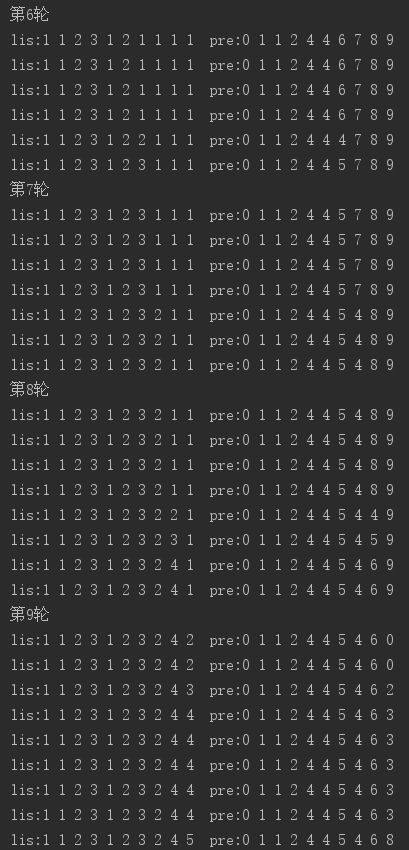
所以第9轮最后这行的lis值以及pre值就是该序列最终的lis和pre。
接下来进入这个循环。1
2
3
4
5
6
7
8for(int k=0;k<lis.length;k++)
{
if(lis[k]>max){
max=lis[k];
index=k;
System.out.print(index+" ");
}
}
这个循环就是为了找出lis数组中最大的值,并对最大值所在下标进行存储,至于找出具体元素的工作就交给pre数组处理。1
2
3
4
5
6
7
8
9Stack<Integer> stack=new Stack<>();
while(index!=pre[index]){
stack.push(array[index]);
index=pre[index];
}
if(index==pre[index])
stack.push(array[index]);
while(!stack.isEmpty())
System.out.print(stack.pop()+" ");
此处使用了一个栈对元素进行存放,实现的效果就如之前所说,当下标没有与pre数组中存储的值重合的时候就一直向前追溯。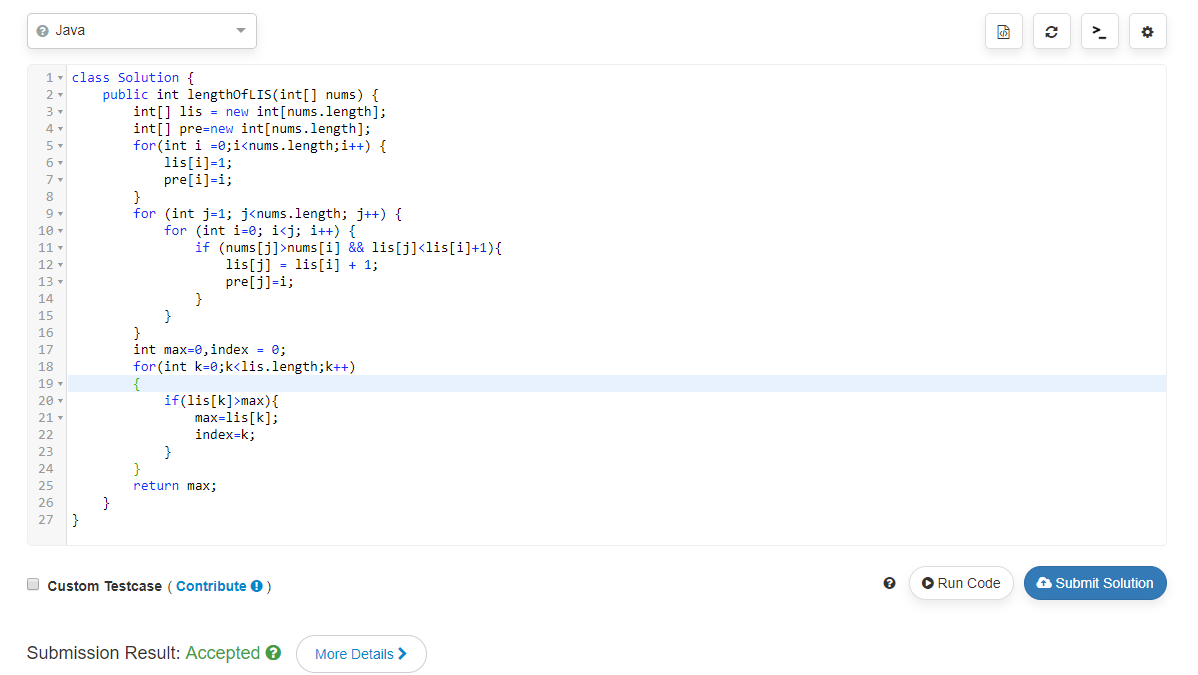
最长长度的计算已经通过leetcode测试
https://leetcode.com/problems/longest-increasing-subsequence/description/。